Jack in the Box - Dynamics Simulation

Overview

Animation

The jack in the box starts with solving the Euler-Langrange eqquations to get the equations of motion. From there, it is required to have 16 impact update equations and conditions to successfully determine if the jack has came into contact with the box. An animation function is also required to visualize these impacts. I chose to represent the jack tips as point masses. Due to the weight of my jack and box, my jack spun very quickly when an impact occured.

Frames

Frames

The frames are defined above. The world {W} frame is outlined in blue, box {B} frame in red, and the jack {J} frame in green. A transformation between the world frame and each of the two other frames was needed to calculate the Kinetic Energy for the Euler-Langrange equations and a transformation between the box frame and jack frame was needed to calculate each φ, what position the impact could potentially occur.

Euler-Langrange

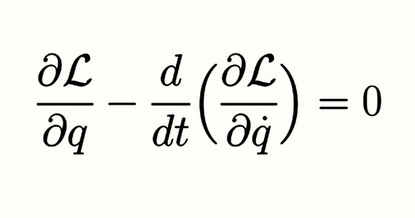
Euler-Lagrange Equation

The Euler-Lagrange equations are a set of differential equations derived from the principle of least action, which is fundamental to classical mechanics. They are used to determine the equations of motion for a system by minimizing the action, which is defined as the integral of the Lagrangian over time. The Lagrangian L is expressed as:

L = T - V

where T and V are the combined kinetic and potential energies of the jack and box. The Euler-Lagrange equations are given by:

∂L/∂q - d/dt (∂L/∂q̇) = 0

for each generalized coordinate q_i​ and its time derivative q̇_i​ (velocity).

In my earlier code implementation, I utilized the Euler-Lagrange (EL) equations to derive the equations of motion for a dynamic system. By defining the Lagrangian as the difference between the kinetic and potential energies, I computed the partial derivatives of the Lagrangian with respect to the generalized coordinates and their time derivatives. These computations allowed me to systematically generate the governing differential equations, which I then solved numerically. Solving the equation gave me q̈, the acceleration of each q.

Impacts

Impact equations were defined for different sides of a box (left, right, top, and bottom). The process involves calculating the influence of external forces and contact points using symbolic matrices to represent transformations and derivatives. For each side of the box, I computed the rate of change in motion (using derivatives with respect to state variables) and balanced them with the forces acting on the system during impact. The symbolic solver helped derive the equations necessary to account for changes in the system’s state due to impacts.

Animation

Other Animations