Kuka YouBot Simulation

Overview

Working Demo

This simulation displays a Kuka Youbot, a 5 axis kinematic arm that sits on a mobile base. The goal of this project was to successfully drive the base to the initial cube, pick it up, and place it at some goal position and orientation. This project utilizes the Modern Robotics library for simplicity in calculating twists, matrix logs, matrix exponentials, inverses, transposes, etc.

Trajectory Generation

Kuka YouBot

To generate trajectories, each frame should be expressed in terms of the s or world frame. Starting from the original frame , 4 more transformation matrices are needed. Respectively, these include the standoff from the intial cube, the intial cube's position, the stand off from the goal position, and the goal position. The states within these matrices were appended to a csv file along with a gripper state. With each of these transformation matrices, a simulation of the gripper can be achieved. In addtion to this,the gripper needed to be closed and opened at the appropiate times. A gripper state was set along with a several copies of the last frame position to ensure that the gripper had enough time to open and close.

Calculating the Next State

This NextState() function computes the next state of a mobile manipulator robot given its current configuration, control inputs, and time step. It updates the robot's arm joint angles, wheel angles, and chassis pose while respecting kinematic constraints and angular velocity limits. By integrating chassis twists and applying forward kinematics, the function provides a seamless simulation of the robot's motion in 3D space.

FeedForward Control

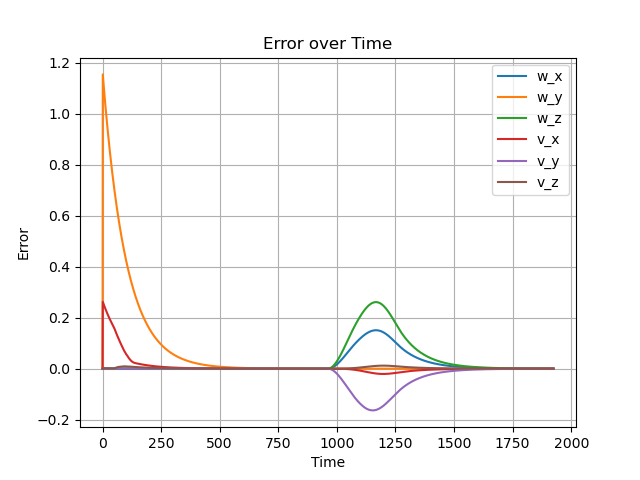
Best Error Over Time

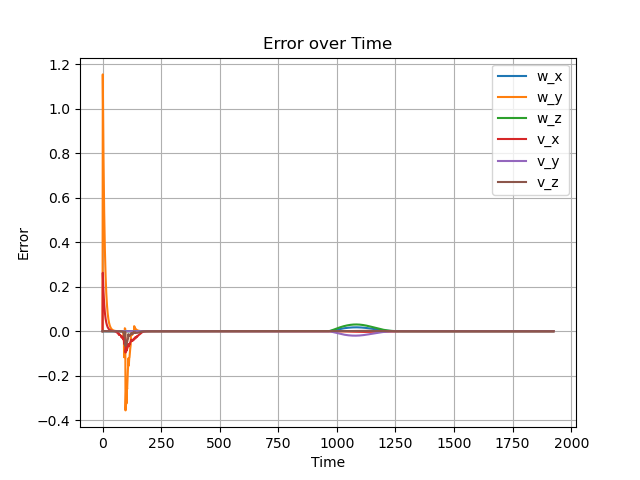
Overshoot